04. The Scale-Free Property ¶

Contents¶

04.01. Introduction
04.02. Power Laws and Scale-Free Networks
04.03. Hubs
- 04.03.01. The Largest Hub
04.04. The Meaning of Scale-Free
04.05. Universality
04.06. Ultra-Small Property
04.07. The Role of the Degree Exponent
04.08. Generating Networks with Arbitrary Degree Distribution
04.09. Summary
04.10. Homework
04.11. Advanced Topic 3.A Power Laws
04.12. Advanced Topic 3.B Plotting Power-laws
04.13. Advanced Topic 3.C Estimating the Degree Exponent
04.14. Bibliography

04.01. Introduction ¶

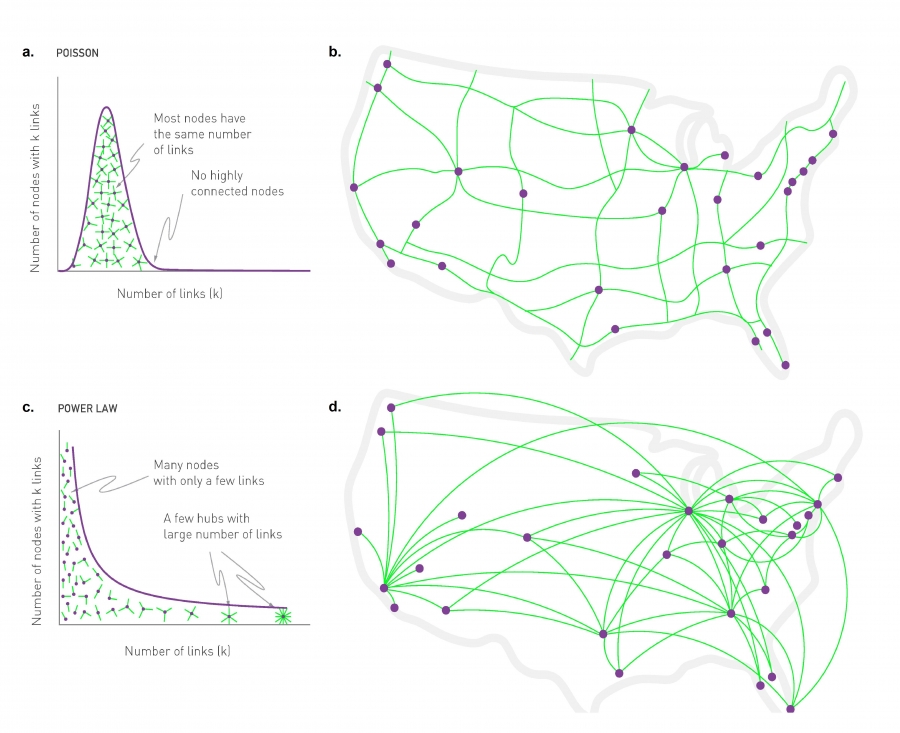
scale-free vs. random network

highly connected; hubs forbidden vs. small-degree, few hubs w/ large number of links

scale-free network

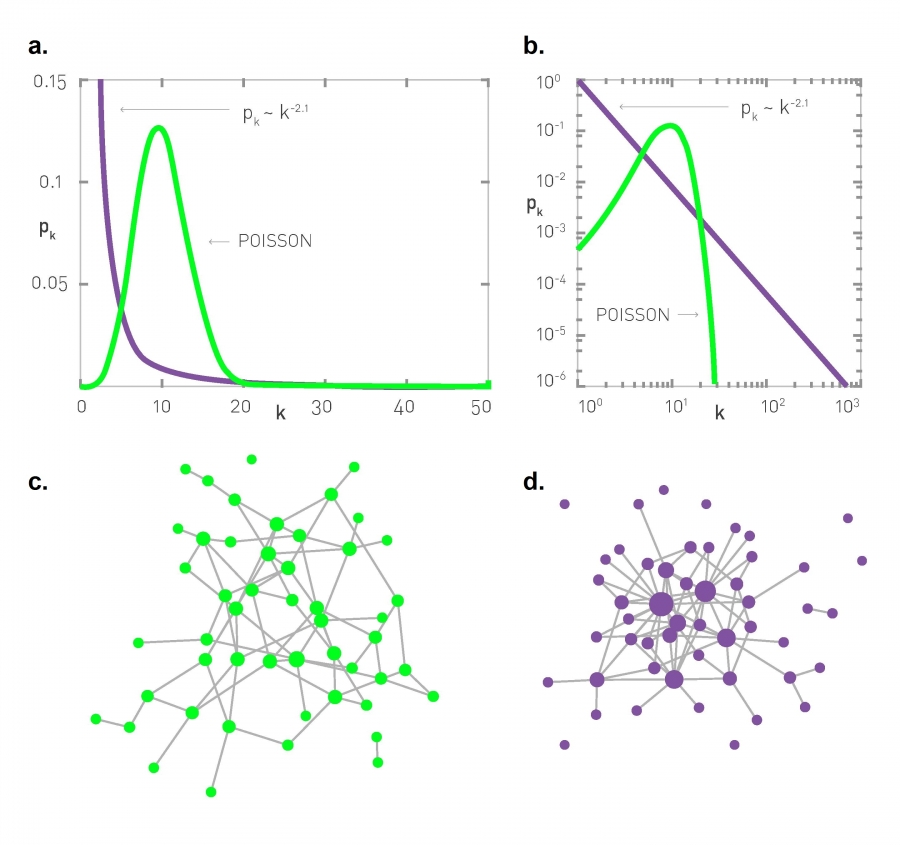
04.02. Power Laws and Scale-Free Networks ¶

fig.4.2 indicates

$p_k \sim k^{-\gamma} \tag{4.1}$

eq.4.1: power law dist

degree exponent $\gamma$

$\log{p_k} \sim - \gamma \log{k} \tag{4.2}$

$\log{p_k}$ depends linealy on $\log{k}$

$γ_{in} = 2.1$ , $γ_{out} = 2.45$
$\langle k_{in} \rangle = \langle k_{out} \rangle = 4.60$

out-degree $k_{out}$ , in-degree $k_{in}$

$p_{k_{in}} \sim k^{- \gamma_{in}} \tag{4.3}$

$p_{k_{out}} \sim k^{- \gamma_{out}} \tag{4.4}$

$\gamma_{in}$ and $\gamma_{out}$

e.g., $\gamma_{in} \approx 2.1$ , $\gamma_{out} \approx 2.45$

scale-free (Barabási, A.L., Albert R., 1999) defined as:

A scale-free network is a network whose degree distribution follows a power law

04.02.01. Discrete Formalism¶

prob $p_k$ , $k$ links

$p_k = C k^{- \gamma} \tag{4.5}$

constant $C$ is determined by the normalization cond

$\sum_{k=1}^\infty {p_k} = 1 \tag{4.6}$

using eq.4.5,

$C \sum_{k=1}^\infty {k^{- \gamma}} = 1$

hence

$C = \frac{1}{\sum_{k=1}^\infty {k^{\gamma}}} = \frac{1}{\zeta(\gamma)} \tag{4.7}$

Riemann-zeta fn $\zeta(\gamma) = \sum_{k=1}^\infty{\frac{1}{k^{\gamma}}}$

for $k>0$ , the discrete power-law dist:

$p_k = \frac{k^{- \gamma}}{\zeta(\gamma)} \tag{4.8}$

04.02.02. Continuum Formalism¶

$p(k) = C k^{- \gamma} \tag{4.9}$

using normalization condition

$\int_{C_{min}}^\infty{p(k)} \mathrm{d}k = 1 \tag{4.10}$

eq.4.9
obtain

$\begin{align*} \int_{k_{\min}}^\infty{p(k)} \mathrm{d}k &= \int_{k_{\min}}^\infty{Ck^{-\gamma}} \mathrm{d}k \\ 1 &= C \int_{k_{\min}}^\infty{k^{-\gamma}} \mathrm{d}k \end{align*}$

$C = \frac{1}{\int_{k_{min}}^\infty{k^{-\gamma} \mathrm{d}k}} = (\gamma - 1) k_{min}^{\gamma - 1} \tag{4.11}$

$p(k) = (\gamma - 1) k_{min}^{\gamma - 1} k^{-\gamma} \tag{4.12}$

$\int_{k_1}^{k_2}{p(k)} \mathrm{d}k \tag{4.13}$

randamly chosen node has degree $[k_1, k_2]$

Box 04.01. The 80/20 Rule and the Top One Percent¶

04.03. Hubs ¶

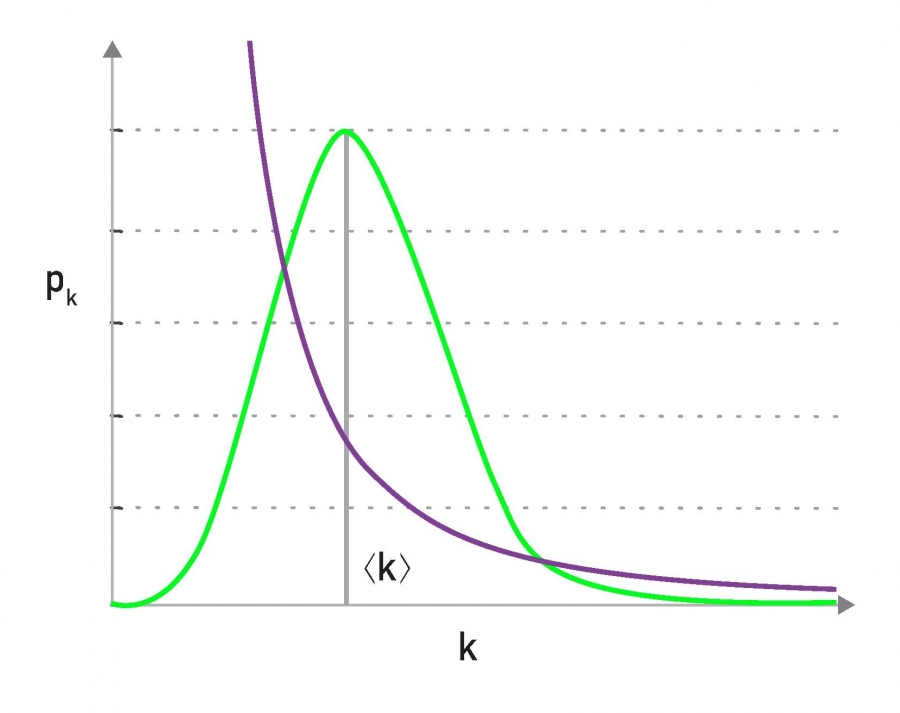
high- $k$ region of $p_k$

for small $k$ , power law is above the Poisson fn
for $k$ in the vicinity of $\langle k \rangle$ , $k \approx \langle k \rangle$
for large $k$ ,

prob (node with $k=100$ )
$p_{100}\approx 10^{-94}$ in Poisson dist
$p_{100} \approx 4 \times 10^{-4}$ in power law

if WWW be random network w/ $\langle k \rangle = 4.6$ , size $N\approx10^{12}$

$N_{k \ge 100} = 10^{12} \sum_{k=100}^\infty{\frac{(4.6)^k}{k!} e^{-4.6}} \simeq 10^{-82} \tag{4.14}$

04.03.01. The Largest Hub¶

WWW is estimated to be $N \approx 10^{12}$ nodes
Earth;s population about $N \approx 7 \times 10^9$
human cell $N \approx 20000$ genes

maximum degree $k_{\max}$ natural cutoff of the degree dist $p_k$

exponential dist

$p(k) = Ce^{- \lambda k}$

minimum degree $k_{\min}$

$\int_{k_{\min}}^\infty{p(k)} \mathrm{d}k = 1 \tag{4.15}$

∵

$\begin{align*} \int_{k_{\min}}^\infty{C e^{- \lambda k} dk} &= 1 \\ \Bigg[ - \frac{1}{\lambda} C e^{- \lambda k} \Bigg]_{k_{\min}}^\infty &= 1 \\ \Bigg( -\frac{1}{\lambda} C e^{- \lambda\times\infty} \Bigg) - \Bigg( -\frac{1}{\lambda} C e^{- \lambda k_{\min}} \Bigg) &= 1 \\ 0 + \frac{1}{\lambda} C e^{- \lambda k_{\min}} &= 1 \\ \Rightarrow C &= \lambda e^{\lambda k_{\min}} \end{align*} \tag{4.15.1}$

eq.4.15 provide $C = \lambda e^{\lambda k_{\min}}$

$k_{\max}$ is $\frac{1}{N}$ :

$\int_{k_{\min}}^\infty{p(k) \mathrm{d}k} = \frac{1}{N} \tag{4.16}$

eq.4.16 yields

$k_{\max} = k_{\min} + \frac{\ln{N}}{\lambda} \tag{4.17}$

$\ln{N}$

$k_{\max} = k_{\min} N^{\frac{1}{\gamma-1}} \tag{4.18}$

04.04. The Meaning of Scale-Free ¶

$n$ ^th moment of the degree distribution is def'd as

$\langle k^n \rangle = \sum_{k_{\min}}^\infty{k^n p_k} \approx \int\limits_{k_{\min}}^\infty{k^n p(k)}dk \tag{4.19}$

lower moments:

$n=1$ : 1st moment is average $\langle k \rangle$
: 2nd moment, ,
- calculate variance $\sigma^2 = \langle k^2 \rangle - \langle k \rangle ^2$
- standard deviation $\sigma$
$n=3$ : 3rd moment, $\langle k^3 \rangle$ , determine skewness of distribution: how symmetric is $p_k$ around the average $\langle k \rangle$

for scale-free network

$\langle k^n \rangle = \int\limits_{k_{\min}}^{k_{\max}}{k^n p(k) dk} = C \frac{k_{\max}^{n - \gamma + 1} - k_{\min}^{n - \gamma + 1}}{n - \gamma + 1} \tag{4.20}$

while $k_{\min}$ is fixed, $k_{\max}$ increases w the system size
$k_{\max} \to \infty$

if $n - \gamma + 1 ≤ 0$ , $k_{\max}^{n - \gamma + 1} \to 0$ , $\langle k^n \rangle \to \text{finite}$
if $n - \gamma + 1> 0$ , $\langle k^n \rangle \to \infty$

many scale-free netw $\gamma \in (2,3)$ ,
$\langle k \rangle \to \text{finite}$ , $\langle k^2 \rangle, \langle k^3 \rangle \to \infty$

Random netw have a scale

$\sigma_k = \langle k \rangle^{\frac{1}{2}}$

in range $k = \langle k \rangle \pm \langle k \rangle^{\frac{1}{2}}$

Scale-free netw lack a scale

power-law degreee dist w $\gamma < 3$
1st moment: finite
2nd moment: infinite

e.g., WWW sample
$\langle k \rangle = 4.60$ , $\gamma\approx2.1$

04.05. Universality ¶

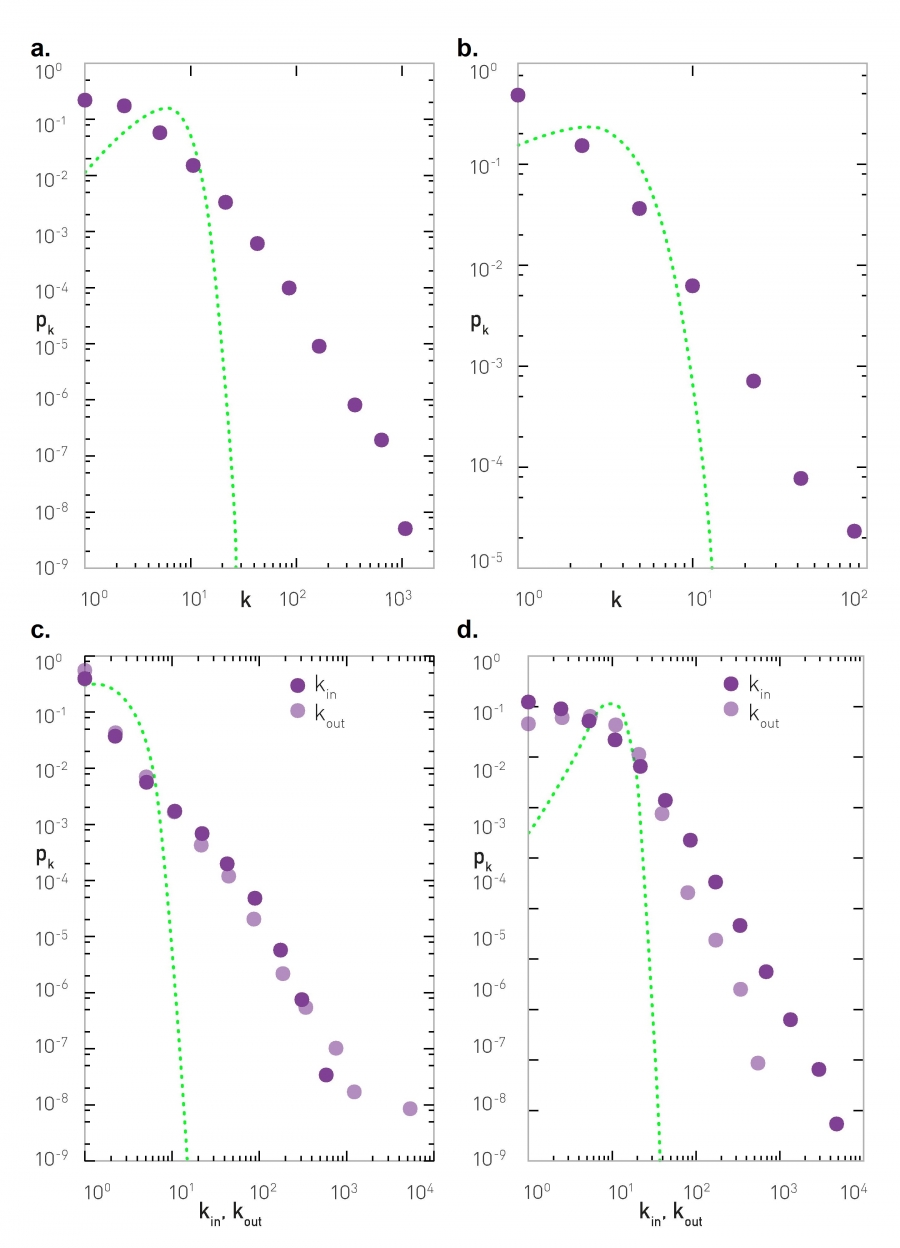
04.05.01. Plotting the Degree Distribution¶

log-log plot

05.14. ADVANCED TOPICS 4.B

04.05.02. Measuring the Degree Exponent¶

05.15. ADVANCED TOPICS 4.C

04.05.03. The Shape of $p_k$ for Real Networks¶

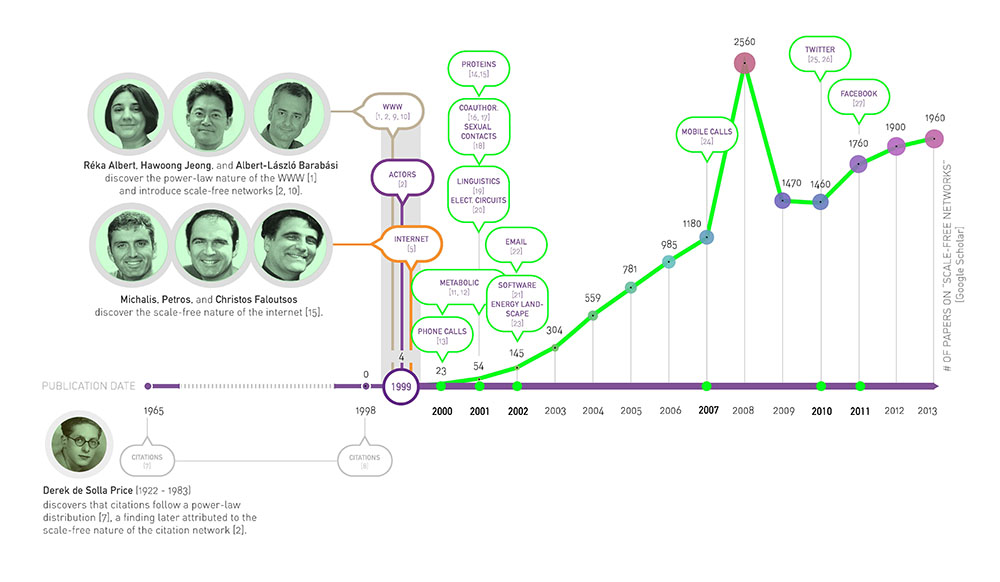
Box 04.02. Timeline: Scale-Free Networks¶

Box 04.03. Not All Network Are Scale-Free¶

NOT all real networks are scale-free

atoms in cystalline / amorphpus matrials
neural network of C. elegans (Amaral, L.A.N., et al., 2000)
power grid

04.06. Ultra-Small Property ¶

hubs affect the small world property?

average distance $\langle d \rangle$ ,
system size $N$ ,
degree exponent $\gamma$

$\langle d \rangle \sim \begin{cases} \text{const.} & \gamma = 2 \\ \ln{\ln{N}} & 2 < \gamma < 3 \\ \frac{\ln{N}}{\ln{\ln{N}}} & \gamma = 3 \\ \ln{N} & \gamma > 3 \end{cases} \tag{4.22}$

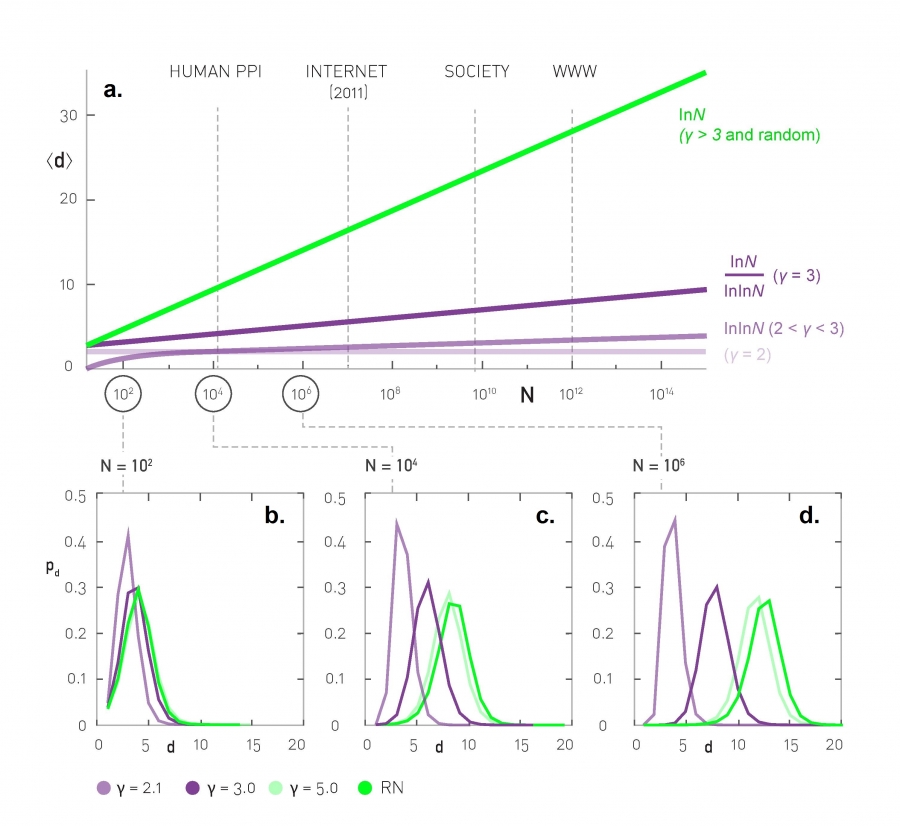
04.06.01. Anomalous Regime ( $γ = 2$ )¶

according to eq.4.18 for $\gamma = 2$

$k_{\max} \sim N$

04.06.02. Ultra-Small World ( $2 < γ < 3$ )¶

eq.4.22

$\ln{\ln{N}}$

Contents¶

04.02.01. Discrete Formalism¶

04.02.02. Continuum Formalism¶

Box 04.01. The 80/20 Rule and the Top One Percent¶

04.03.01. The Largest Hub¶

04.05.01. Plotting the Degree Distribution¶

04.05.02. Measuring the Degree Exponent¶

04.05.03. The Shape of p_k for Real Networks¶

Box 04.02. Timeline: Scale-Free Networks¶

Box 04.03. Not All Network Are Scale-Free¶

04.06.01. Anomalous Regime (γ = 2)¶

04.06.02. Ultra-Small World (2 < γ < 3)¶

04.06.03. Critical Point (γ = 3)¶

04.06.04. Small World (γ > 3)¶

Box 04.04. We Are Always Close to the Hubs¶

04.07. The Role of the Degree Exponent¶

Box 04.05. The γ Dependent Properties of Scale-Free Networks¶

04.07.01. Anomalous Regime (γ ≤ 2)¶

04.07.02. Scale-Free Regime (2 < γ < 3)¶

04.07.03. Random Network Regime (γ > 3)¶

Box 04.06. Why Scale-Free Networks With γ < 2 Do Not Exist¶

04.08. Generating Networks with Arbitrary Degree Distribution¶

04.08.01. Configuration Model¶

Box 04.07. Generating a Degree Sequence with Power-Law Distribution¶

04.08.02. Degree-Preserving Randomization¶

04.08.03. Hidden Parameter Model¶

Box 04.08. Testing the Small-Word Property¶

04.09. Summary¶

04.09.01. Exponentially Bounded Networks¶

04.09.02. Fat Tailed Networks¶

Box 04.09. At a Glance: Scale-Free Networks¶

04.10. Homework¶

04.11. Advanced Topic 3.A Power Laws¶

04.11.01. Exponentially Bounded Distributions¶

04.11.02. Fat Tailed Distributions¶

04.11.03. Crossover Distribution (Log-Normal, Stretched Exponential)¶

Box 04.10. Degree Distribution of Real Networks¶

04.12. Advanced Topic 3.B Plotting Power-laws¶

04.12.01. Use a Log-Log Plot¶

04.12.02. Avoid Linear Binning¶

04.12.03. Use Logarithmic Binning¶

04.12.04. Use Cumulative Distribution¶

04.13. Advanced Topic 3.C Estimating the Degree Exponent¶

04.13.01. Fitting Procedure¶

04.13.02. Goodness-of-fit¶

04.13.03. Fitting Real Distributions¶

04.13.04. Systematic Fitting Issues¶

04.14. Bibliography¶

04.05.03. The Shape of $p_k$ for Real Networks¶

04.06.01. Anomalous Regime ( $γ = 2$ )¶

04.06.02. Ultra-Small World ( $2 < γ < 3$ )¶

04.06.03. Critical Point ( $γ = 3$ )¶

04.06.04. Small World ( $γ > 3$ )¶

Box 04.05. The $γ$ Dependent Properties of Scale-Free Networks¶

04.07.01. Anomalous Regime ( $γ ≤ 2$ )¶

04.07.02. Scale-Free Regime ( $2 < γ < 3$ )¶

04.07.03. Random Network Regime ( $γ > 3$ )¶

Box 04.06. Why Scale-Free Networks With $γ < 2$ Do Not Exist¶