03. Bifurcations¶
Contents¶
- 03.00. Introduction
- 03.01. Saddle-Node Bifurcation
- 03.02. Transcritical Bifurcation
- 03.03. Laser Threshold
- 03.04. Pitchfork Bifurcation
- 03.05. Overdamped Bead on a Rotating Hoop
03.00. Introduciton¶
birfurcation
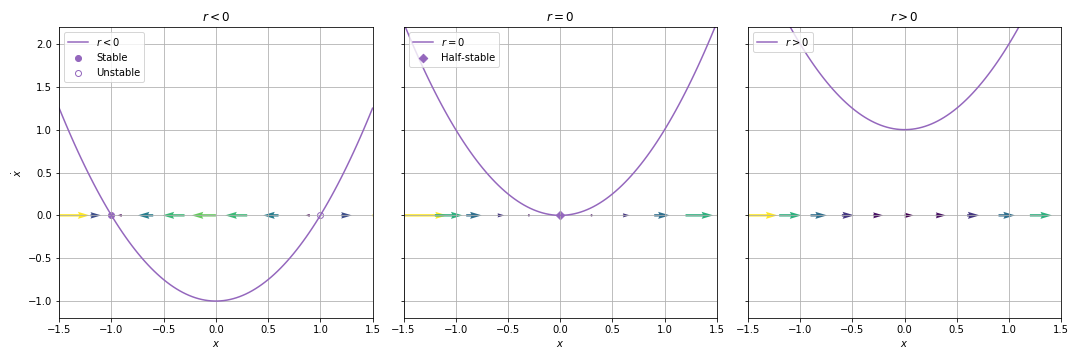
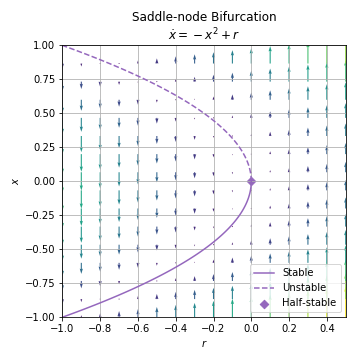
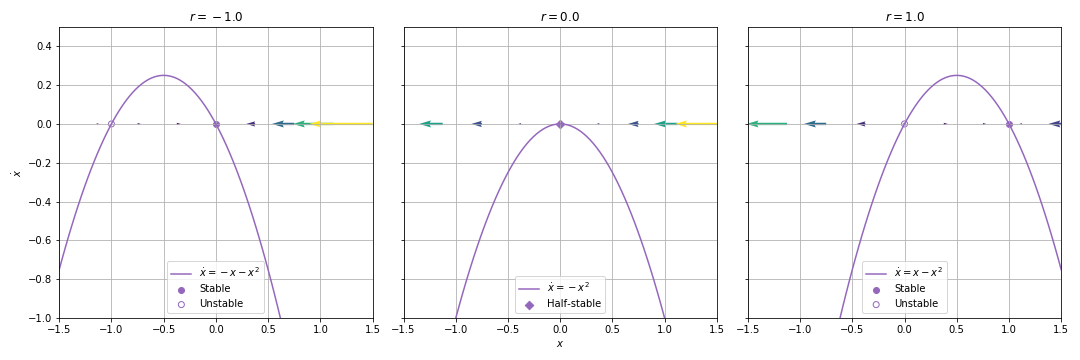
03.01. Saddle-Node Bifurcation¶
03.01.01. Graphical Conventions¶
bifurcation diagram
03.01.01.01. Terminology¶
fold bifurcation (aka, tuning-point bifurcation, blue sky bifurcation)
[Abraham, Shaw (1988)][1988_Shaw_Abraham]
Example 03.01.01.¶
linear stability analysis of fixed point:
Solution
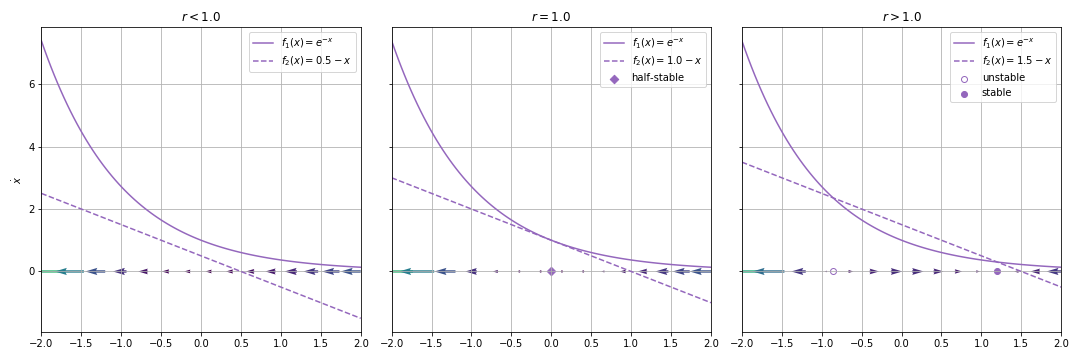
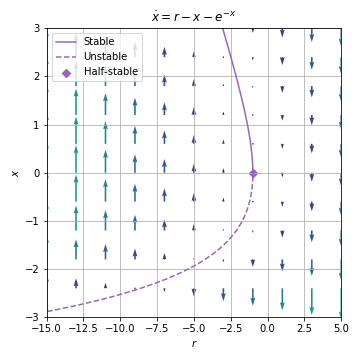
Example 03.01.02.¶
Solution:
derivative:
and
,
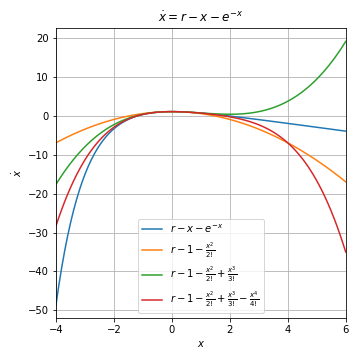
03.01.02. Normal Forms¶
Taylor expansion
bifurcation at , Taylor's expansion
(⇐ is fixed point),
where ,
normal forms
Guckenheimier, Holmes (1983), Wiggins (1990)
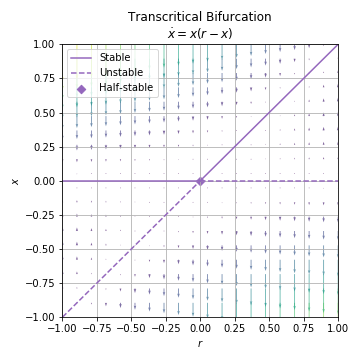
03.02. Transcritical Bifurcation¶
transcritical bifurcation
Example 03.02.01.¶
show the first-order system
Solution:
Example 03.02.02.¶
analyze
near
Solution:
and
(Guckenheimer and Holmes (1983), Wiggins (1990), Manneville (1990))
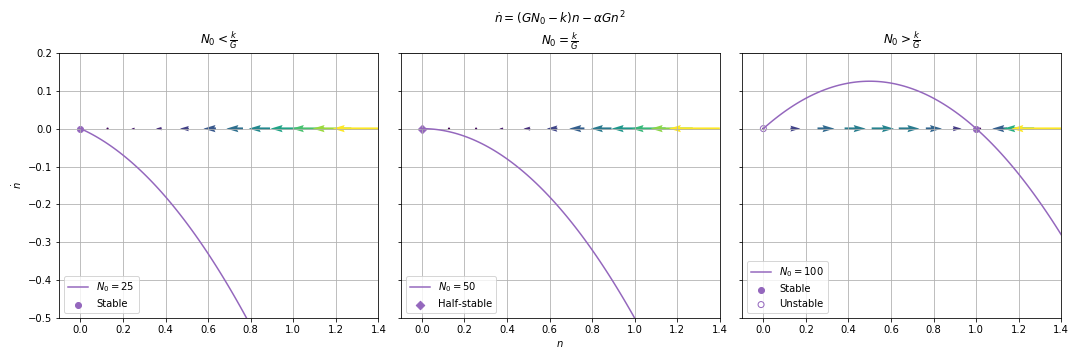
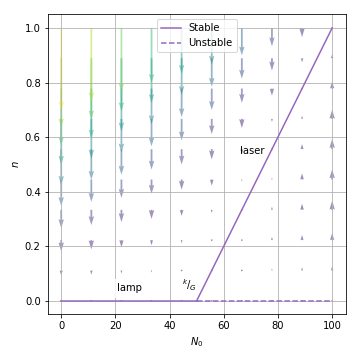
03.03. Laser Threshold¶
03.03.01. Physical Background¶
solid-state laser
03.03.02. Model¶
: num of photons
simulated emission
- : num of excited atoms
- : gain coef
- : rate constant;
- : lifetime of photon in laser
- : rate at which atoms drop back to graund state
Substitute:
03.04. Pitchfork Bifurcation¶
Pitchfork bifurcation
symmetry
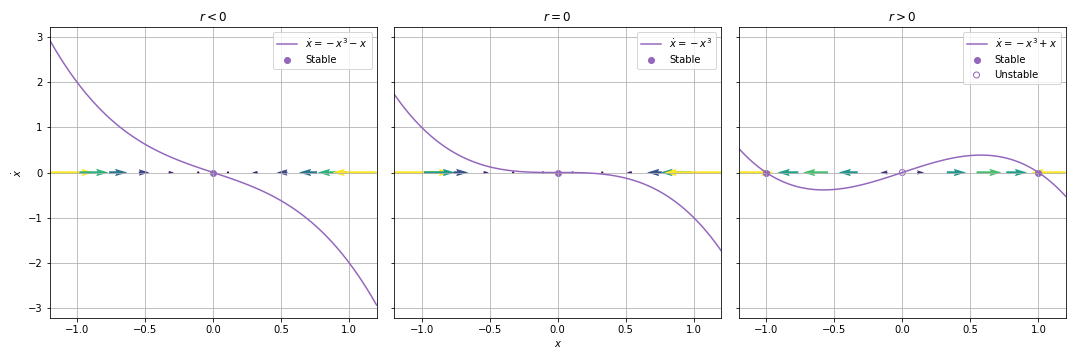
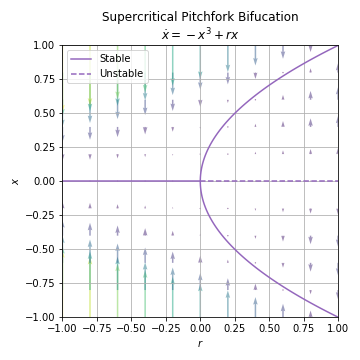
03.04.01. Supercritical Pitchfork Bifurcation¶
Example 03.04.01.¶
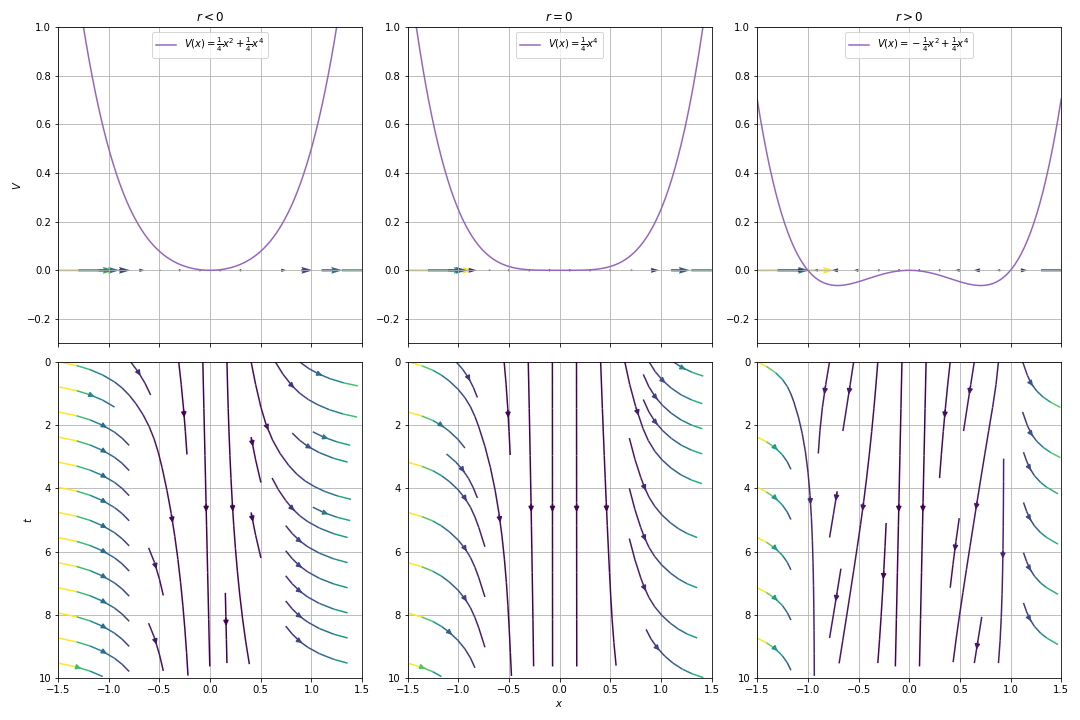
Example 03.04.02.¶
Plot potential for the system
Solution
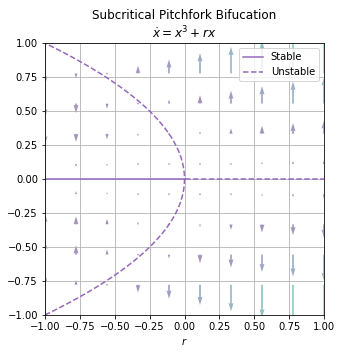
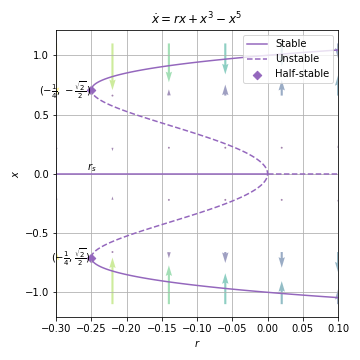
03.04.02. Subcritical Pitchfork Bifurcation¶
03.04.03. Terminology¶
- Supercritial pitchfork
- aka, Forward bifurcation
- soft/safe
- Subcritical pitchfork
- aka, Backward bifurcation
- hard/dangerous
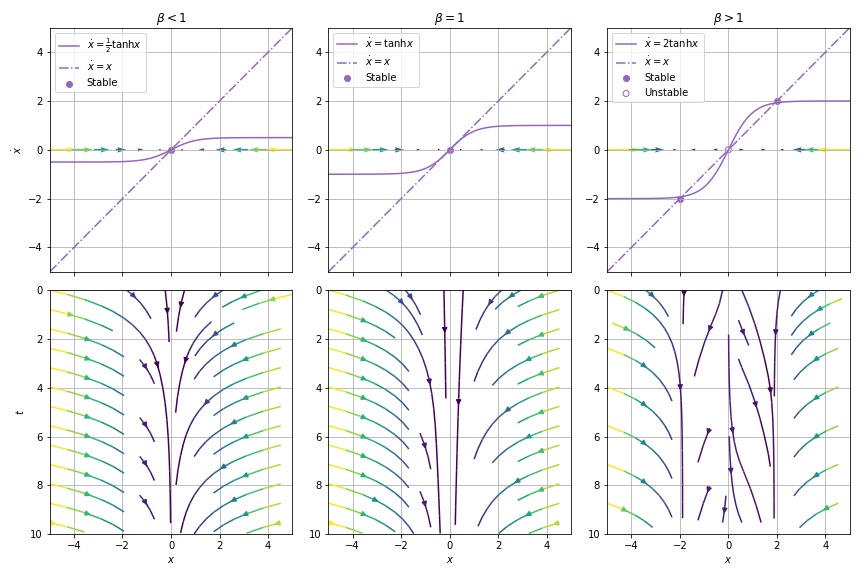
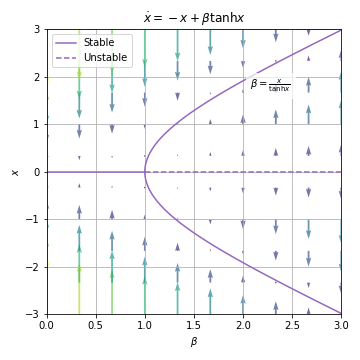
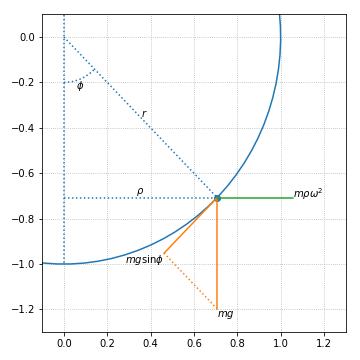
03.05. Overdamped Bead on a Rotating Hoop¶
Let
- : angle ()
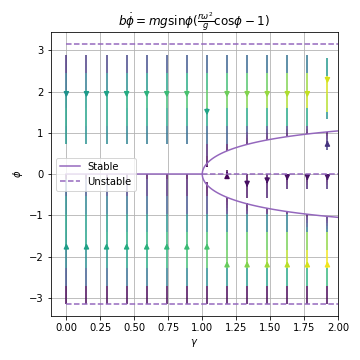
03.05.01. Analysis of the First-Order System¶
where ,
additional fixed points, if
introduce param ,
solve
03.05.02. Dimensional Analysis and Scaling¶
when valid to neglect the inertia term ?
dimensionless form (C.C. Lin and L.A. Segel (1988))
dimentionless time
,
Characteristic time scale
substitute for
(3)
needed
dumping is strong; mass is small
(3) becomes