02. Flows on the line¶

ToC¶

• 02.00. Introduction
• 02.01. A Geometric way of Thinking
• 02.02. Fixed Points and Stability
  • Example 2.2.1
  • Example 2.2.2
  • Example 2.2.3
• 02.03. Population Growth
  • 02.03.01. Critique of the Logistic Model
• 02.04. Linear Stability Analysis
  • Example 2.4.1
  • Example 2.4.2
  • Example 2.4.3
• 02.05. Existence and Uniquness
  • Example 2.5.1
  • Example 2.5.2
• 02.06. Impossibility of Oscillations
  • 02.06.01. Mechanical Analog: Overdamped Systems
• 02.07. Potentials
  • Example 2.7.1
  • Example 2.7.2
• 02.08. Solving Equations on the Computer
  • 02.08.01. Euler's Method
  • Example 2.8.1

02.00. Introduction¶

general system

$$\begin{align*} \dot{x}_1 &= f_1(x_1, \cdots, x_n) \\ & \vdots \\ \dot{x}_n &= f_n(x_1, \cdots, x_n) \end{align*}$$

simple case $n = 1$

$$\dot{x} = f(x)$$

one-dimensinal / first-order system

02.01. A Geometric way of Thinking¶

$$\dot{x} = \sin x \tag{1}$$

$$dt = \frac{dx}{\sin x}$$

implies:

$$\begin{align*} t &= \int \csc x \, \mathrm{d}x \\ &= - \ln |\csc x + \cot x | + C \end{align*}$$

$$t = \ln \Big|\frac{\csc x_0 + \cot x_0}{\csc x + \cot x}\Big| \tag{2}$$

fixed point:

• stable
• unstable

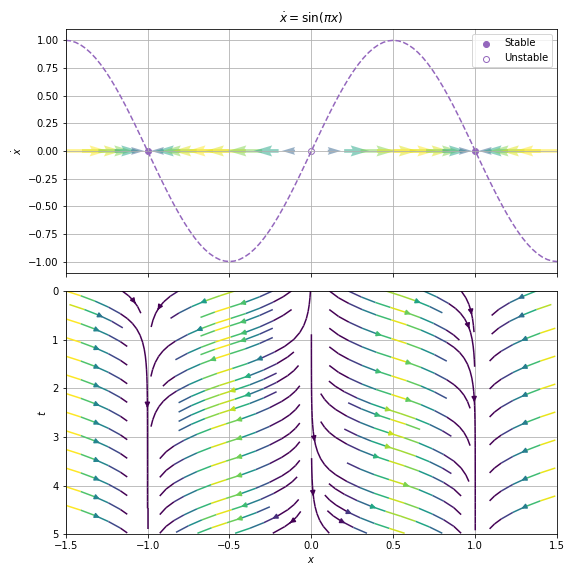
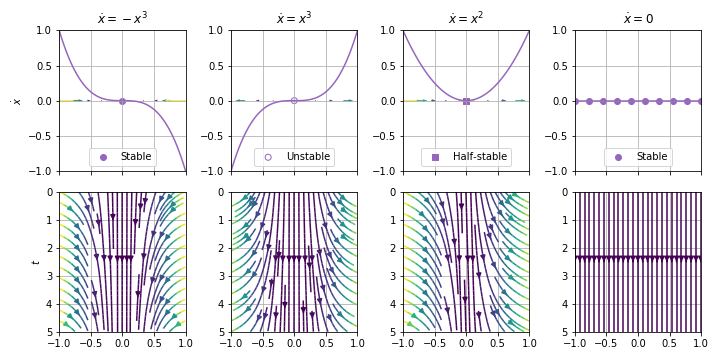
02.02. Fixed Points and Stability¶

• phase point: imaginary point
• phase portrait: qualitatively different trajectories

Example 2.2.1¶

$$\dot{x} = x^2 - 1$$

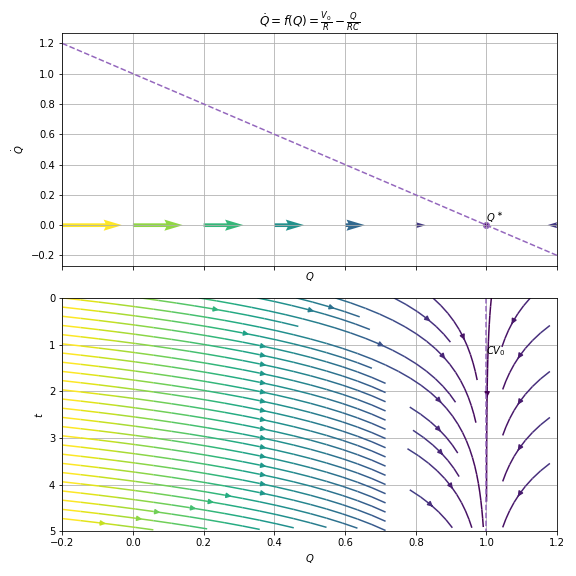
Example 2.2.2¶

resistor $R$, capacitor $C$, voltage $V_0$

let $Q(t)$ denote the charge on the capacitor at time $t≥0$

Solution

$$-V_0 + RI + \frac{Q}{C} = 0$$

$$\dot{Q} = I$$

hence

$$- V_0 + R\dot{Q} + \frac{Q}{C} = 0$$ or $$\dot{Q} = f(Q) = \frac{V_0}{R} - \frac{Q}{RC}$$

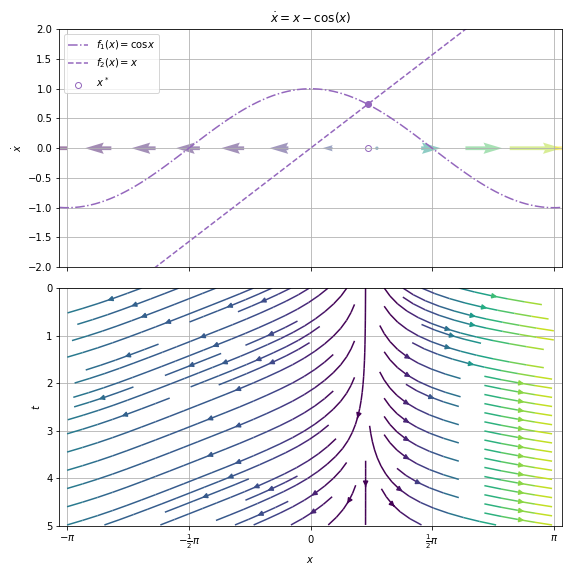
Example 2.2.3¶

$$\dot{x} = x - \cos{x}$$

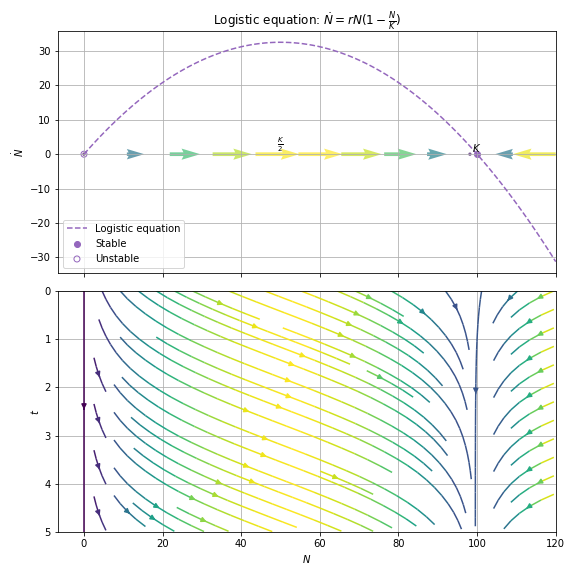
02.03. Population Growth¶

$$\dot{N} = rN$$

growth rate $r$

$$N(t) = N_0e^rt$$

Carrying capacity: $K$

Logistic eq

$$\dot{N} = rN \Big(1 - \frac{N}{K} \Big)$$

02.03.01. Critique of the Logistic Model¶

originally, univeral law of growth ([Pearl, 1927][1927_Pearl])

• bacteria, yeast: sigmoid growth curve
• fruit flies, flour beetles: perssistent fluctuation ⇐ age structure, time-delayed effect ([Krebs, 1972][1972_Krebs])

[Pielou 1969], [May 1981], [Edelstein=Keshet 1988], [Murray 2002], [Murray 2003]

02.04. Linear Stability Analysis¶

Let

• $x^\ast$: fixed point

$$\eta(t) = x(t) - x^\ast$$

$$\dot{\eta} = \frac{d}{dt} (x - x^\ast) = \dot{x}$$

$x^\ast$ is constant

$$\dot{\eta} = \dot{x} = f(x) = f(x^\ast + \eta)$$

Taylor's expansion:

$$f(x^\ast + \eta) = f(x^\ast) + \eta f'(x^\ast) + O(\eta^2)$$

• $O(\eta^2)$: quadratically small term in $\eta$

$$\dot{\eta} = \eta f'(x^\ast) + O(\eta^2)$$

$$\dot{\eta} \approx \eta f'(x^\ast)$$

linearization about $x^\ast$

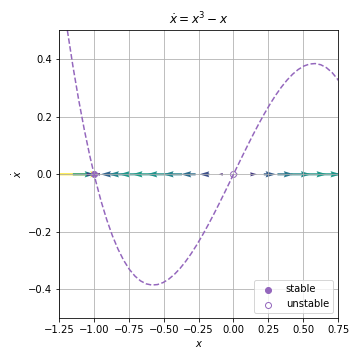
Example 2.4.1¶

using linear stability analysis:

$$\dot{x} = \sin{x}$$

Solution:

$$\begin{align*} f'(x^\ast) &= \cos k\pi \\ &= \begin{cases} 1, &\quad k \text{ even} \\ -1, &\quad k \text{ odd} \end{cases} \end{align*}$$

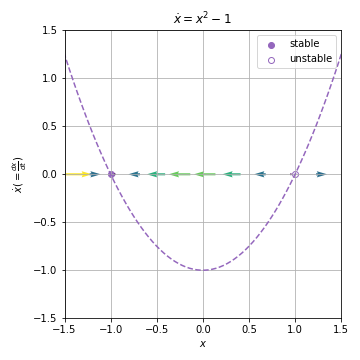
Example 2.4.2¶

using linear stability analysis

Solution:

$$f(N) = rN (1 - \frac{N}{K})$$

fixed points $N^* = 0$, $N^* = K$

$$f'(N) = r - \frac{2rN}{K}$$

$f'(0) = r$, $f'(K) = -r$

characteristic time scale is $\frac{1}{|f'(N^\ast)|} = \frac{1}{r}$

Example 2.4.3¶

1. $\dot{x} = - x^3$
2. $\dot{x} = x^3$
3. $\dot{x} = x^2$
4. $\dot{x} = 0$

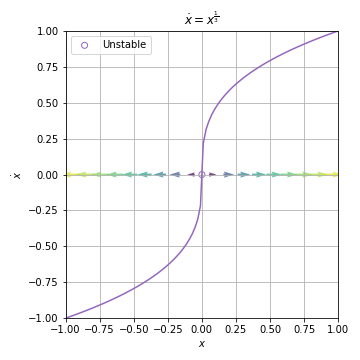
02.05. Existence and Uniquness¶

$\dot{x} = f(x)$

Example 2.5.1¶

$$\dot{x} = x^{\frac{1}{3}}$$

Solution:

$$\int x^{-\frac{1}{3}} dx = \int dt$$

$$\frac{3}{2} x^{\frac{2}{3}} = t + C$$

Example 2.5.2¶

$$\begin{align*} \dot{x} &= 1 + x^2 \\ x(0) &= x_0 \end{align*}$$

solutions exist for all time?

Solution:

consider the case where $x(0)=0$

solved analytically

$$\int{\frac{dx}{1 + x^2}} = \int{dt}$$

yeilds

$$\tan^{-1}{x} = t + C$$

$x(0) = 0$ implies $C = 0$

solution exists for $-\frac{\pi}{2} < t < \frac{\pi}{2}$, because $x(t) \rightarrow \pm\infty$ as $t \rightarrow \pm\frac{\pi}{2}$

02.06. Impossibility of Oscillations¶

02.06.01. Mechanical Analog: Overdamped Systems¶

$\dot{x} = f(x)$ can't oscillate limiting case of Newton's law

intertia term $m\ddot{x}$ is negligible

$$m\ddot{x} + b\dot{x} = F(x)$$

$b\dot{x} \gg m\ddot{x}$

behave like $b \dot{x} = F(x)$

02.07. Potentials¶

another way to visualize 1st-order system $\dot{x} = f(x)$

potentials $V(x)$ is defined by

$$\dot{x} = f(x) = - \frac{dV}{dx}$$

$$\frac{dV}{dt} = \frac{dV}{dx} \frac{dx}{dt}$$

$$\frac{dx}{dt} = - \frac{dV}{dx}$$

$$\frac{dV}{dt} = - \Big( \frac{dV}{dx} \Big)^2 ≤ 0$$

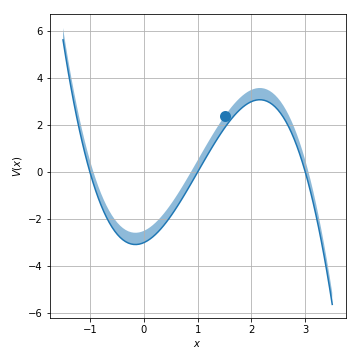
Example 2.7.1¶

Graph the potential fot the system: $\dot{x} = - x$

Solution:

$- \frac{dV}{dx} = -x$

general solution: $V(x) = \frac{1}{2} x^2 + C$

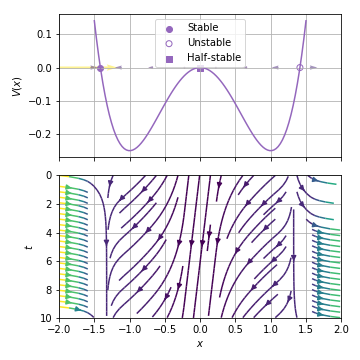
Example 2.7.2¶

Graph the potential for the system: $\dot{x} = x - x^3$

identify all equibrium points

Solution:

$-\frac{dV}{dx} = x-x^3$

yeilds

$$V = -\frac{1}{2} x^2 + \frac{1}{4} x^4 + C$$

double-well potential

bistable

02.08. Solving Equations on the Computer¶

• graphical
• analytical
• numerical method

numerical intergration

02.08.01. Euler's Method¶

$$\dot{x} = f(x)$$

$$\begin{align*} x(t_0 + \Delta t) &\approx x_1 \\ &= x_0 + f(x_0) \Delta t \end{align*}$$

$$x_{n+1} = x_n + f(x_n) \Delta t$$

fourth-order Runge-Kutta method

$$\begin{cases} k_1 = f(x_n) \Delta t \\ k_2 = f(x_n + \frac{1}{2} k_1) \Delta t \\ k_3 = f(x_n + \frac{1}{2} k_2) \Delta t \\ k_4 = f(x_n + k_3) \Delta t \\ \end{cases} \\ x_{n+1} = x_n + \frac{1}{6} (k_1 + 2 k_2 + 2 k_3 + k_4)$$

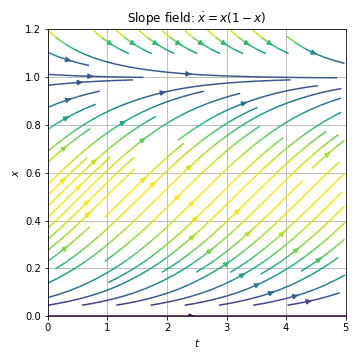
Example 2.8.1¶

Solve the system $\dot{x} = x (1 - x)$ numerically

Solution:

¶